
順列と組み合わせについて解説します。
この範囲は「データサイエンティストのためのスキルチェックリスト」の「データサイエンス力」項目No.1の解説になります。
多くの専門用語や公式が登場しますが丁寧に理解しやすく説明していきます。
本記事はデータサイエンスを研究されているIffat Maabさんによる英語の解説を翻訳しています。
Iffat Maab
東京大学大学院工学系研究科技術経営戦略学専攻(TMI)博士課程在学中。パキスタン、イスラマバード市出身
マーケターのためのデータサイエンスの時間とは?
こちらの講座では、一般社団法人データサイエンティスト協会様がリリースしている「データサイエンティストのためのスキルチェックリスト」に沿った解説を行っていきます。
「データサイエンティストのためのスキルチェックリスト」とは、データサイエンティストとして活躍するために必要なスキルが体系化されたものです。
このマーケターのためのデータサイエンスの時間に従って学習していくと、データサイエンティストに必要なスキルセットである「データサイエンス力」を一通り学習することが出来ます。
<マーケターのためのデータサイエンスの時間の全一覧はこちら>
順列や組合せを式 nPr, nCr を用いて計算できる。
解答
順列の式
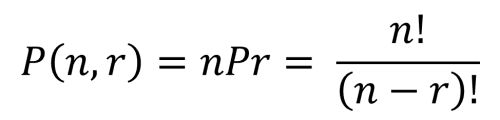
組合せの式
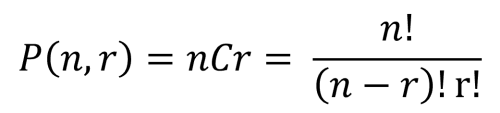
解説
こちらは順列と組合せに関する問いです。
順列と組合せは混乱することが多いと思います。
そのため、混乱しないように多くの具体例を用いて解説していきます。
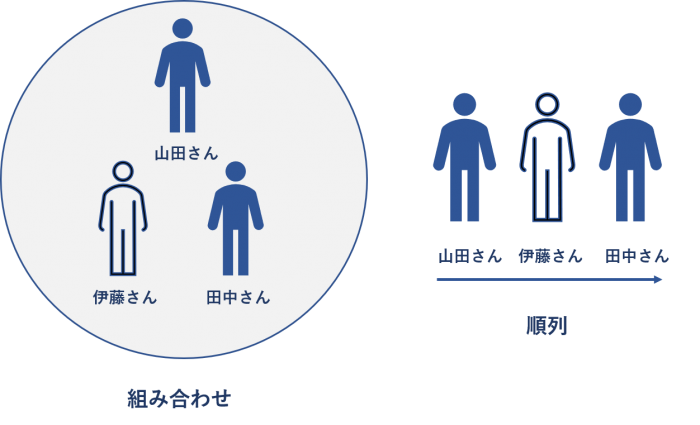
例えば、「山田さん、伊藤さん、田中さん」という3人の名前について見てみましょう。
上の名前の並び方は、「伊藤さん、田中さん、山田さん」とは異なります。
このように順番が重要になるときが【順列】です。1列に並べる際の並べ方の事をいいます。
順列は順序が重要な問題のためのものですが、一方で【組合せ】では順序は重要ではありません。
例えば、組合せでは、「山田さん、伊藤さん、田中さん」の順番がどのようであっても構わないのです。
つまり、この3人が要素として、含まれていることが重要なのです。
そして、この順列と組合せの違いをより理解するために、もう一つ例を説明します。
例えば、私の携帯電話のパスワードが3478であるとしましょう。
パスワードは正確には3-4-7-8でなければなりません。
3487やその他のパスワードの数字の順番ではないので、ここでは順番が重要です。つまり、順列であり、組み合わせではありません。
順列の公式
n個のものの中から、r個を選んで一列に並べる際の並べ方の数はこちらの公式で求めることが出来ます。
組み合わせは英語でパーミュテーション(Permutation)なので、簡略化して頭文字のPで表されています。
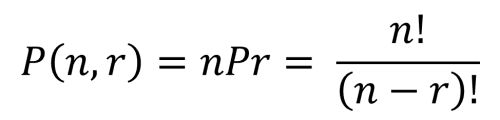
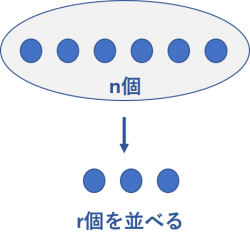
全てのものを並べる際は、n!になります。!とは階乗と読み、全ての数字をかけるという意味です。
例えば、3!=3×2×1
6!=6×5×4×3×2×1
といった計算を行います。
順列の問題例
問題
8人の選手がレースをする場合、金メダル、銀メダル、銅メダルを渡す方法は何通りあるでしょうか。
解答
この例題では、選手の総数は8人なので、n = 8になります。
この例題では、金、銀、銅の3つのメダルを8人の選手に渡す方法が何通りあるかを聞いています。
メダルの総数は3個なので、一度に3個のメダル(物)を並べることになるので、r=3となります。
式を使って
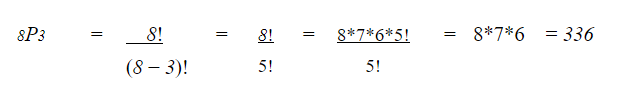
つまり、8人のプレーヤーに金メダル、銀メダル、銅メダルを与える方法は336通りあるということになります。
組合せの公式
順番が問題にならない場合、それが組合せです。
組合せは英語でコンビネーション(combination)なので、頭文字のCで表されます。
正確には数学で、n個のものをr個取ったときの組み合わせの数は、次の式で求められます。
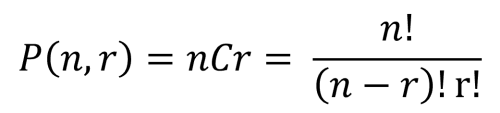
組合せの例(1)
問題
5つの果物の中から4個取るときの組み合わせは何通りでしょうか。
解答
この例では、全部で5つの物があるので、n=5です。
ここで、4つのものを一度に取る際の組み合わせの数は、r=4となります。
これらの値を上の式に入れると、
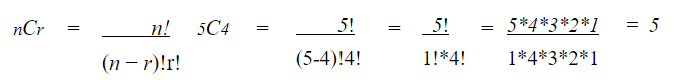
となり5通りであることが分かります。
組合せには順序の制限がないため、組み合わせの総数は順列よりも少ないことがわかります。
組合せの例(2)
問題
10人のグループから3人のチームを選ぶ方法は何通りありますか。
解答
まず、この例題では、3人のチームを選ぶことが求められており、一度に3つのものを扱っていることになるので、r=3となります。
また、1グループの人数は10人なので、n=10となります。
組み合わせ式の値の検討 上の式に値を入れると、組合せの総数は120となり、3人のチームを選ぶ方法が120通りあることになります。
これらの値を上の式に入れると、
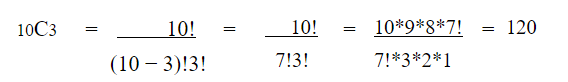
となり、120通りであることが分かります。
まとめ
以上が「データサイエンス力」のNo.1の解説になります。
次回はNo.2からの解説になります。1~271項目まで順に追って解説していくので、マーケターの皆さんは本シリーズを読んで、データサイエンスの世界に踏み出していきましょう。
English
Permutation and combination formulas can be expressed using P, C, m, n
There is always a confusion on which one to use combination or permutation. You can remember by the sounds, permutation sounds complicated, isn’t it? because when you use permutation every little attribute matters. For example the three names, Haleema, Bilal and Nouman are different from Nouman, Bilal and Haleema because now the order matters.
The different ways in which objects from a set are arranged in the form of subsets is done by permutations and combinations. Permutations are for the matters where order is significant whereas in combinations the order doesn’t matter. The password of my mobile phone is 3478. Now the order matters here as the password should exactly be 3-4-7-8 but not 3487 or any other order of the password digits.
Permutation Formula
The number of permutations of ‘n’ objects taken ‘r’ at a time is determined by the following formula:
Permutation Example # 1
In how many different orders can three runners named A, B , C finish a race if no ties are allowed?
Solution
The different orders for runners A, B, and C are
ABC, ACB, BAC, BCA, CAB, CBA
Here in this example the total number of elements are three i.e., A , B, C which means n = 3. Now the question says that in how many different orders the three runners are arranged so r also becomes 3 i.e., r = 3, also r = n. ‘r’ tells the number of objects taken at a time and we are taking all the runners at a time for order arrangement. Hence the following computation is made:
| nPr | = |
n! (n − r)! |
= |
n! (n − n)! |
= |
n! 0! |
= |
n! 1 |
= | n! |
nPn is the number of permutations of n different things taken n at a time, it is the total number of permutations of n things i.e., n!
| 3P3 | = |
3! (3 − 3)! |
= |
3! 0! |
= |
3! 1 |
= | 6 |
As mentioned earlier, the 6 different orders of permutations for the three runners are ABC, ACB, BAC, BCA, CAB, CBA
Permutation Example # 2
If there are eight players running a race, then how many ways are there to give out the gold, silver, and bronze medals.
Solution
In this example the total number of players are eight, so n = 8. The example says how many different ways the three medals gold, silver and bronze will be given to the eight players. The total number of medals are three so we are taking three medals (objects) at a time to arrange, so r = 3. Using the formula
| 8P3 | = |
8! (8 − 3)! |
= |
8! 5! |
= |
8*7*6*5! 5! |
= | 8*7*6 | = 336 |
So there are 336 different ways to give gold, silver and bronze medals to the eight players.
Combination Formula
When the order doesn’t matter, it is a Combination “C”. Precisely in Mathematics, the number of combinations of ‘n’ objects taken ‘r’ at a time is determined by the following formula:
Combination Example # 1
How many combinations are there of 5 distinct things taken 4 at a time?
Solution
In the given example, there are a total of five things so n = 5. Now the number of combinations for arranging four things at a time means r = 4. Putting the values in the above formula
| nCr | = |
n! (n − r)!r! |
5C4 | = |
5! (5-4)!4! |
= |
5! 1!*4! |
= |
5*4*3*2*1 1*4*3*2*1 |
= 5 |
Due to no restriction of order in the combination, you can see that the total number of combinations are less than the permutations. This is because in combination, ABC is exactly the same as CBA or any other sequence provided that there is no restriction in the question.
Combination Example # 2
How many ways are there to pick a team of 3 people from a group of 10.
Solution
In this example, it is asked to pick a team of 3 people which means at a time we are dealing with 3 objects, hence r = 3. Now the total number of people in a group is 10, so n = 10. Examining the values in the combination formula Putting the values in the above formula will give a total combination of 120 which means there are a possible number of 120 ways in which a team of three members can be chosen.
| 10C3 | = |
10! (10 − 3)!3! |
= |
10! 7!3! |
= |
10*9*8*7! 7!*3*2*1 |
= | 120 |
Purpose
Also note that permutation and combination is a unitless quantity. Permutations and combinations are highly used in statistics, communication networks, cryptography, network security, and computer architecture etc.
Suppose you are ready to launch a new product and are trying to figure out the best strategy on how to announce it to the general public [3c]. You’ve identified four different marketing strategies that you are considering to undertake.
- Send a press release and schedule interviews with the news media
- Run an online marketing campaign
- Run a TV/ radio marketing campaign
- Sponsor and speak at an industry conference
From your experiences in marketing, you believe that the order in which you undertake these initiatives matters. In other words, you think that the outcome that would come about by running an online marketing campaign before sponsoring and speaking at an industry conference would be different than if the conference happened before the online marketing campaign.
So how many different outcomes do you have to consider? This is an example of permutations without replacement as discussed earlier.
There are now four different strategies to consider, which we will denote as n = 4. When thinking about what to do first, you have four choices. When thinking about what to do second, you only have three choices left (since we aren’t going to check the same marketing strategy twice). At the time you are making the choice of what to do third, you have two strategies remaining. Finally, the strategy to do last is determined by your previous choices as there is only one option left. Putting all this together, you have 4 * 3 * 2 * 1 = 24 different outcomes to consider which gets calculated through permutation.

