ベイズの定理【マーケターのためのデータサイエンスの時間】

ベイズの定理について解説します。

この範囲は「データサイエンティストのためのスキルチェックリスト」の「データサイエンス力」項目No.13の解説になります。

多くの専門用語や公式が登場しますが丁寧に理解しやすく説明していきます。

本記事はデータサイエンスを研究されているIffat Maabさんによる英語の解説を翻訳しています。

 

Iffat Maab

東京大学大学院工学系研究科技術経営戦略学専攻（TMI）博士課程在学中。パキスタン、イスラマバード市出身

---

マーケターのためのデータサイエンスの時間とは？

こちらの講座では、一般社団法人データサイエンティスト協会様がリリースしている「データサイエンティストのためのスキルチェックリスト」に沿った解説を行っていきます。

「データサイエンティストのためのスキルチェックリスト」とは、データサイエンティストとして活躍するために必要なスキルが体系化されたものです。

 

このマーケターのためのデータサイエンスの時間に従って学習していくと、データサイエンティストに必要なスキルセットである「データサイエンス力」を一通り学習することが出来ます。

＜マーケターのためのデータサイエンスの時間の全一覧はこちら＞

---

ベイズの定理を説明できる

解答

ベイズの定理とは現在の結果から過去の原因の確率を導く為の定理である。条件付確率の公式を変形させたものであり、公式は以下のようになっている。

 

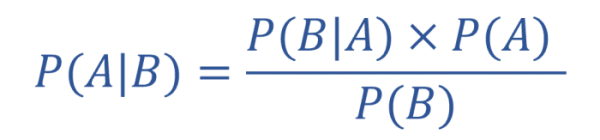
解説

ベイズの定理とは確率の分野に属している定理であり、機械学習の基礎にもなっています。

そこで、ベイズの定理は難しそうな名前とは裏腹にイメージを持つことで簡単に理解することが出来ます。

 

ベイズの定理のイメージとしては「結果から原因を推定する」ことになります。

一般的な確率では、降水確率やサイコロで5が出る確率など「未来を予測する」ことに用いられていると思います。

しかし、ベイズの定理では現在の結果から過去の原因の確率を導くという違いがあります。

例えば、以下のような問題でベイズの定理を用います。

---

«以下のようにビー玉が袋に入っており、いずれかの袋からビー玉を１つ取り出したらそのビー玉が青でした。

このビー玉が袋Ｂから取り出された確率はいくらでしょうか。

袋Ａ：赤いビー玉が2つ、青いビー玉が１つ

袋Ｂ：赤いビー玉が1つ、青いビー玉が2つ»

---

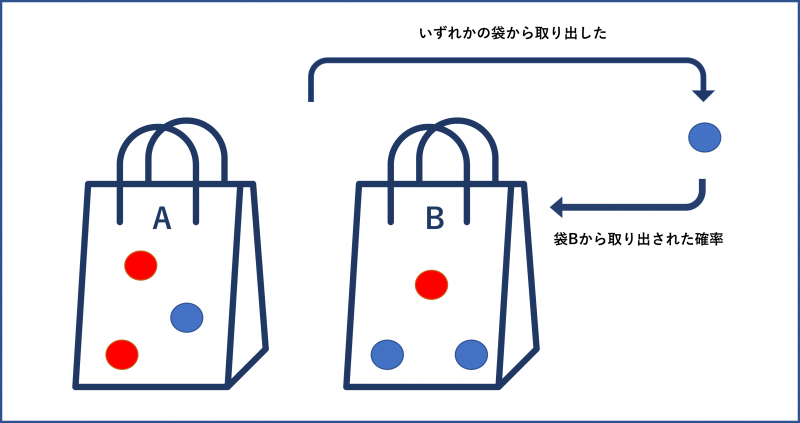
この問題から分かるように、既に起きた事象の原因の確率を求めていることが分かります。

ベイズの定理では、一般的な確率とは異なり過去を推測する時に用いるのです。

従って、ベイズの定理を扱う時はこの時間の感覚を持つことが大切になっています。

 

ベイズの定理のイメージが掴めたところで、ベイズの定理の求め方を説明します。

端的には、条件付き確率の公式を変形させることでベイズの定理になります。

条件付確率の公式はこちらです。

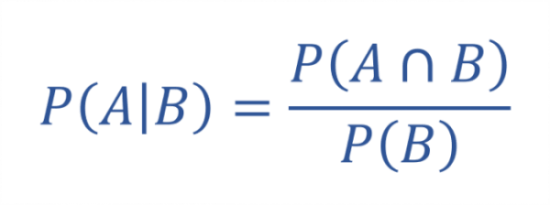
事象Ｂが起こったという条件で事象Ａが起こる確率です。条件付き確率についてはこちらの記事で解説しているのでご確認下さい。

以下の2つの手順でベイズの定理を求めることが出来ます。

①乗法定理を求める

ここでP(A∩B)は事象Ａと事象Ｂが同時に起こる確率になっています。

そこで一度、条件付確率の公式をP(A∩B)=P(A|B)×P(B)という式に変形させます。

ここで、P(B)とP(A)を入れ替えてP(A∩B)=P(A|B)×P(A)にします。このＡとBを入れ替えることは乗法定理の性質として理解して下さい。

ちなみに、この変形した式は乗法定理と呼ばれており導かずに覚えておくと便利になっています。

②乗法定理を条件付確率の公式に代入

条件付確率の公式のP(A∩B)に乗法定理を代入します。

 

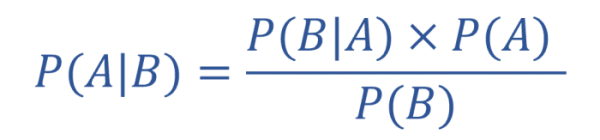
これがベイズの定理になっています。

機械学習はベイズの定理を用いて学習していることもあり理解しておきましょう。

 

そして、先ほどの問題を実際に解いてみましょう。

袋Aから青が取り出された確率は1/3

袋Bから青が取り出された確率は2/3　です。

さらに、袋は2つしかないため袋Aから取り出された確率は1/2、袋Bから取り出された確率も1/2です。

これらをベイズの定理に当てはめた結果、答えは2/3　になります。

---

まとめ