単回帰分析と重回帰分析

単回帰分析と重回帰分析とは

両者は回帰分析に属する分析手法です。
簡潔に表すと以下のようになります。

回帰分析
単回帰分析	重回帰分析
1つの変数によって、予測値や因果関係を導き出す分析手法。	2つ以上の変数によって、予測値や因果関係を導き出す分析手法。

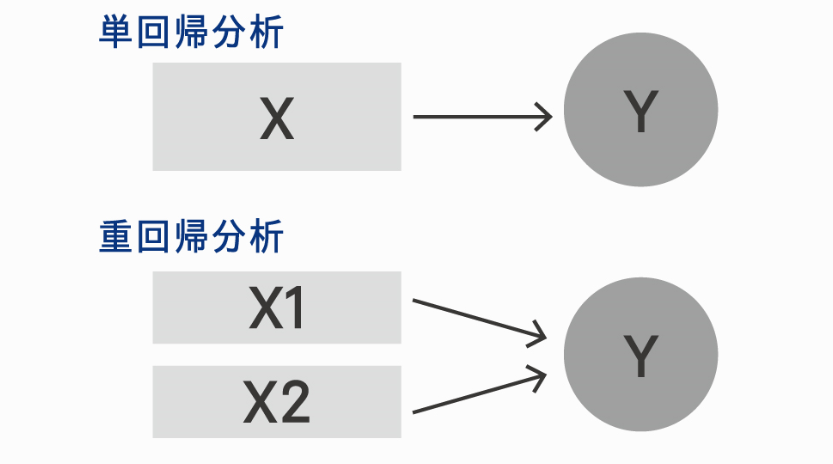
単回帰分析と重回帰分析の具体例

家賃が決まる決定要因をそれぞれの手法を使って以下のように分析できます。
（実際には数値で分析します。）

	独立変数（※1）	従属変数（※2）	傾向
単回帰分析	「駅からの距離」	「家賃」	駅からの距離が近いほど家賃が高くなる傾向。
重回帰分析	「駅からの距離」 「築年数」	「家賃」	駅からの距離が近いほど、築年数が短いほど、家賃が高くなる傾向。

※1・・・独立変数とは、予測値や因果関係を説明する変数のことです。説明変数、予測子変数と呼ぶこともあります。一般的には、「x」で表されることが多いです。
※2・・・従属変数とは、説明変数によって決定される変数のことです。目的変数、応答変数と呼ぶこともあります。一般的には、「y」で表されることが多いです。

上記は具体例は数値を出さずに説明しました。
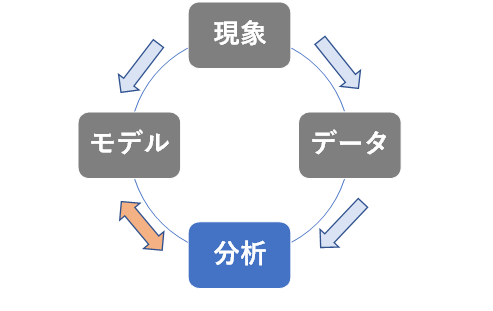
ただ実際の回帰分析は、現象から得たデータを分析して意味を持つモデルを作り出し、モデルを介して現象のある側面を近似的に理解します。

回帰モデルと線形回帰モデル

単回帰分析と重回帰分析を数式的に理解するには回帰モデルが必要です。
回帰モデルとは変数間の関係を表すモデルのうちの1つです。
実際に変数間の関係を回帰モデル式で表すと、下記のようになります。

文字ばかりの数式が並んで難しそうですが、基本的には独立変数「x」によって従属変数「y」が導かれているという関係性を表してるシンプルな式になります。
この回帰モデルにおいて、変数間の関係を下記のように表せるのですが、この時を特に線形回帰モデルと呼びます。

こちらの式を活用することで、単回帰分析と重回帰分析を数式的に理解することが可能になります。

最小二乗法（最小自乗法）

最小二乗法は、回帰モデルを考える際に必ず知っておきたい概念になります。
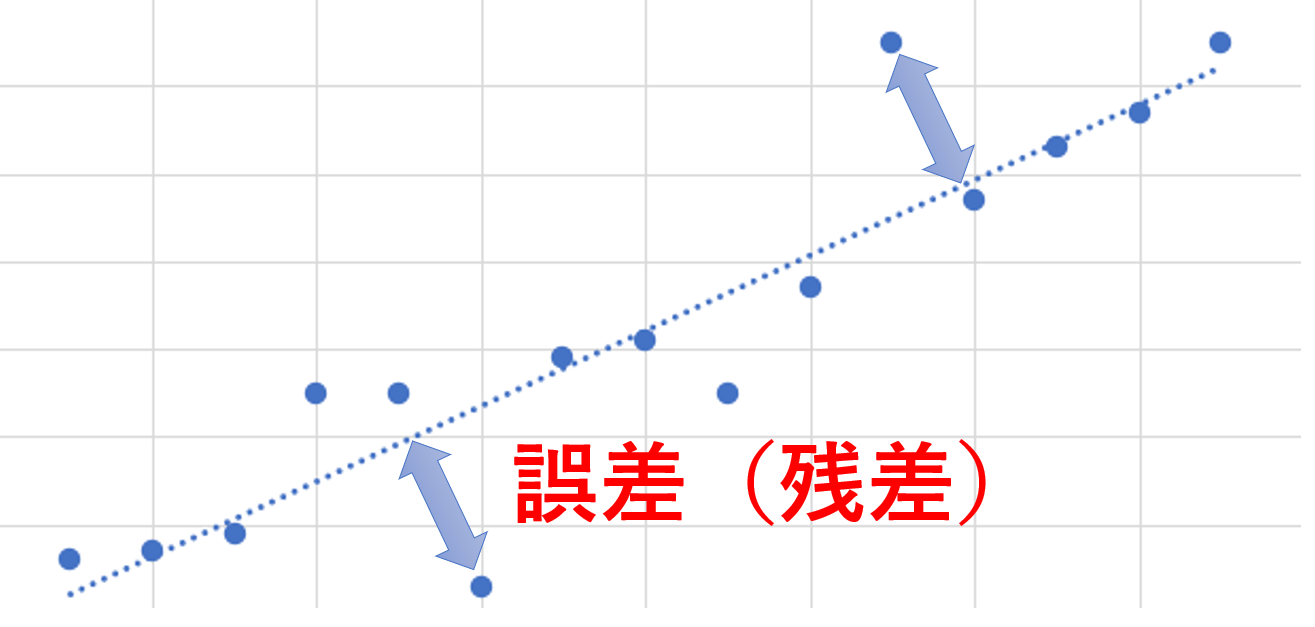
簡潔にいうと、下記の図のような誤差（残差※1）を調節して、最も確からしい関係式に調整する役割があります。

ズレが小さいほど、近似の精度が高いと言えます。

※1・・・残差は実際のデータと予測値との差を指します。

回帰モデルの具体例

単回帰モデル

単回帰モデルの場合は、1つの独立変数xで従属変数yを説明します。そのため、線形回帰モデルは下記のようになります。

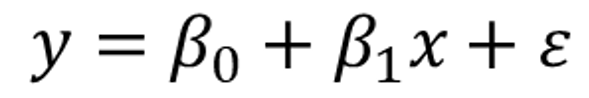
分析の具体例

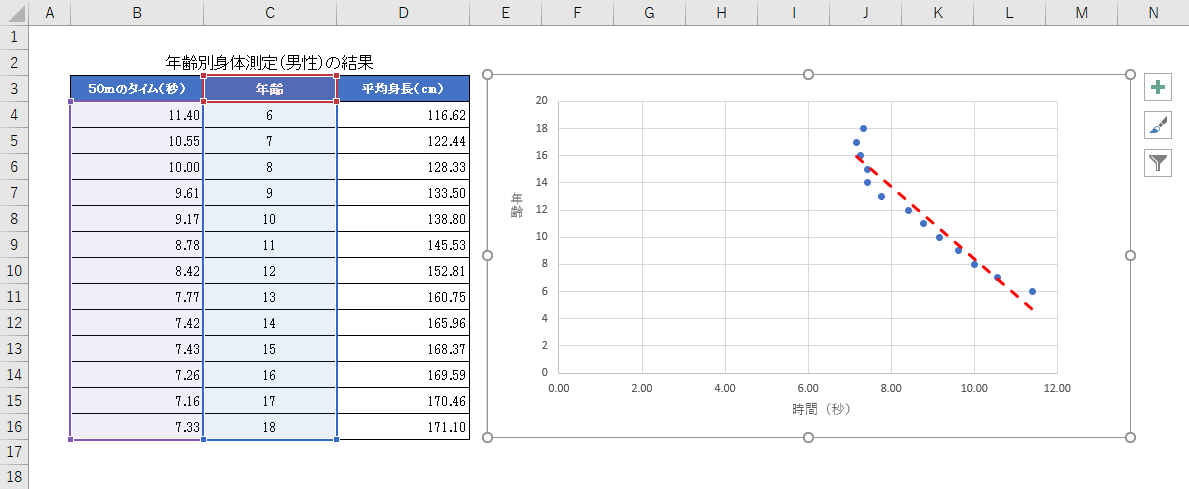
年齢別身体測定（男性）の結果を単回帰分析します。従属変数を「50mのタイム（秒）」、独立変数を「年齢」と設定します。
結果が以下のグラフになります。赤い直線は線形近似した直線となり、上記の式によって導き出された直線になります。
グラフを見ると、年齢が上がるにつれて50mのタイムが速くなる傾向が見えます。

 

データはe-Statより引用。
e-Statは、日本の統計が閲覧できる政府統計ポータルサイト。
参考データは2018年度の「50m走、立ち幅とび、ソフトボール投げ・ハンドボール投げ」と「身長、体重」の統計表シートのデータから抜粋。

単回帰分析の結果によって求める調整された直線の具体的な数値は、エクセルで分析をした際に自動生成される数値から求められます。
今回の単回帰分析によって調整された直線の式は、青色の箇所より切片が12.82、年齢（独立変数x）の係数が-0.35となっていることが読み取れます。（小数第3桁目を四捨五入）
そのため、以下の近似された単回帰モデルが導き出されます。

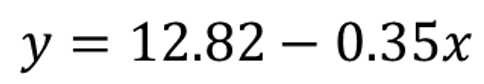
このように意味を持つモデルを作り出し、モデルを介して現象のある側面を近似的に理解します。

重回帰モデル

重回帰モデルの場合は、単回帰モデルと同様に下記の線形回帰モデルを変形させることで求められます。

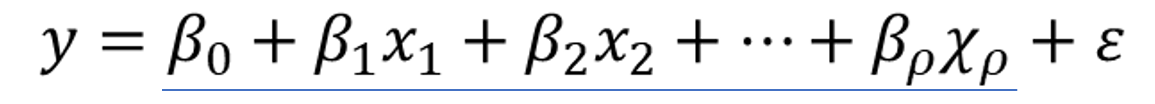今回は下記のように独立変数が2つの場合の式で話を進めます。

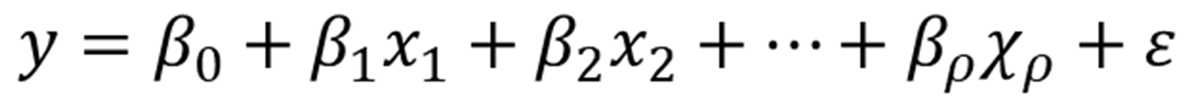
分析の具体例

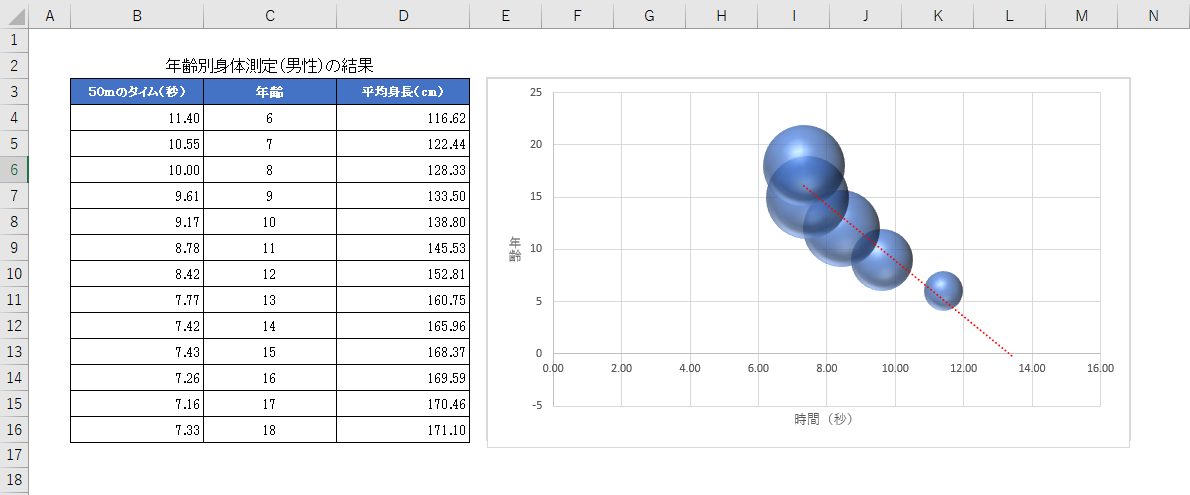
先ほど使用した年齢別身体測定（男性）の結果を重回帰分析します。従属変数を「50mのタイム（秒）」、独立変数を「年齢」「平均身長」と設定します。
その際の結果が以下のグラフになります。赤い直線は線形近似した直線となり、上記の式によって導き出された直線になります。
一生身長が伸び続けたり、50mのタイムが速くなり続けることはないため、上限値と下限値がある前提にはなりますが、グラフからは年齢が上がるにつれて、身長が高くなるにつれて、50mのタイムが速くなる傾向が見えます。
※今回は見やすくお伝えするために、グラフに表示しているデータは6,9,12,15,18歳の抜粋のみ。

重回帰分析の結果によって求める式の具体的な数値は、エクセルで重回帰分析をした際に自動生成される上記のようなシートから求められます。
今回の重回帰分析の式は、青色の箇所より切片が20.464、年齢（独立変数x）の係数が-0.076、平均身長（独立変数x）の係数が-0.085となっていることが読み取れます。（小数第4桁目を四捨五入）
そのため、以下の近似された重回帰モデルが導き出されます。

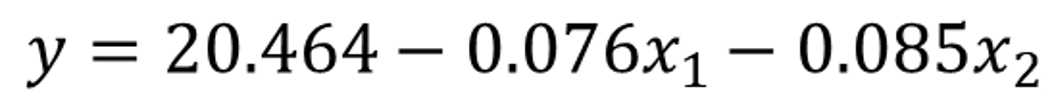
独立変数の数が多いほど様々な要因を考慮していることになりますが、その分モデルも複雑になります。独立変数を複数設定する際は、本当に加えるべき要素なのかどうかを慎重に検討する必要があります。

単回帰分析と重回帰分析の活用事例

単回帰分析と重回帰分析は、マーケティングなどビジネスの現場においてよく活用されています。単回帰分析と重回帰分析はどちらも汎用性が高く、ビジネスだけでなく、実生活上のさまざまな場面で使用されています。

たとえば、アメリカでは重回帰分析を利用した特定地域の寿命予測が行われました。人口や面積、収入などが独立変数として従属変数となる寿命を調査しました。

他には、営業予測にも回帰分析は活用されます。取引額を従属変数とし、訪問回数や値引率等を数値化して分析することで営業戦略が変わった場合の効果の変動などを予測することもできます。

まとめ

単回帰分析と重回帰分析は一見難しそうですが、考え方はシンプルになります。条件を定義してデータを分析し、その結果生じたモデルから事象のある側面を推察します。
エクセルなどのツールを用いることで分析自体は比較的簡単にできますが、どの条件で分析し、生じたモデルをどう解釈するかを考えるのは難しい点です。