母平均と標本平均について解説します。
この範囲は「データサイエンティストのためのスキルチェックリスト」の「データサイエンス力」項目No.5の解説になります。
多くの専門用語や公式が登場しますが丁寧に理解しやすく説明していきます。
本記事はデータサイエンスを研究されているIffat Maabさんによる英語の解説を翻訳しています。
Iffat Maab
東京大学大学院工学系研究科技術経営戦略学専攻(TMI)博士課程在学中。パキスタン、イスラマバード市出身
マーケターのためのデータサイエンスの時間とは?
こちらの講座では、一般社団法人データサイエンティスト協会様がリリースしている「データサイエンティストのためのスキルチェックリスト」に沿った解説を行っていきます。
「データサイエンティストのためのスキルチェックリスト」とは、データサイエンティストとして活躍するために必要なスキルが体系化されたものです。
このマーケターのためのデータサイエンスの時間に従って学習していくと、データサイエンティストに必要なスキルセットである「データサイエンス力」を一通り学習することが出来ます。
母(集団)平均と標本平均、不偏分散と標本分散がそれぞれ異なることを説明できる
解答
母平均は「母集団全体」での平均であるが、標本平均は「母集団から抽出した一部」の平均という違いがある。
そして、標本分散は標本のばらつきを表すもので、不偏分散は標本から偏りを除いて母集団の分散を推定するために表すものである。
解説
こちらは母平均と標本平均の違いと不偏分散と標本分散の違いに関する問いです。
どちらも「平均」と「分散」ですが少し異なっています。今回はそれらの違いを理解しましょう。
母集団と標本の違い
母集団とは、対象となる人、物、項目の集まりです。
一方、標本とは母集団から抽出された一部の集まりです。標本は適切に採取された場合には全体を代表するものになり、母集団の特徴を推測することが出来ます。
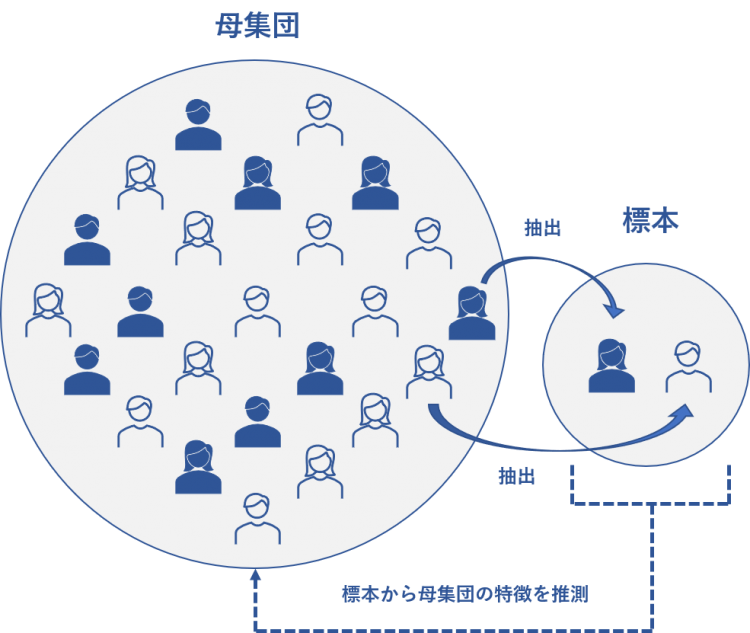
母集団平均
母集団平均は、先ほど説明した対象となる人、物、項目の集まりである母集団の平均です。上の図では左側の集団の平均です。
平均の求め方はこちらの第5回の記事で解説しています。
標本平均
標本平均は,抽出された標本の平均のことを指します。上の図では右側の集団の平均です。
例えば、東京都の野生のネコの平均体重を調べるとします。全てのネコを図ることは不可能なので、東京都の野生のネコを3匹標本として抽出したとします。
そこで、3匹の体重が、
4.0kg、3.7kg、3.9kg であるとします。
この平均は3.86kgとなりますが、この平均は母集団(東京都の野生のネコ)の割合ではありません。
たまたま抽出された標本の平均値が3.86kgであり、このことを標本平均といいます。
標本平均と母集団平均はデータの推論のために必要になっています。
母集団は有限ですが、非常に大きいものになっています。例えば,インドの人口は約14億人と有限ではありますが非常に大きすぎる数値になっています。
このように、通常の場合には調査対象となる母集団データの全てを観察することはできません。
母集団が大きすぎる場合は標本を抽出し、調査することで母集団の統計的な特徴を把握することが可能になっているのです。
標本分散
次に標本分散についてです。標本分散とは名前の通り標本の分散であり、一般的に求め方は普通の「分散」と同じになっています。
母集団の分散は母分散、標本の分散は標本分散と呼びます。
そして、標本分散も母分散と同じようにデータセット内のばらつきを表すために用いられるものです。
【マーケターのためのデータサイエンスの時間】~4限目~で解説しているように、分散は以下の公式を持っています。
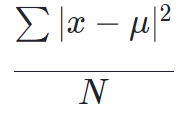
この(標本)分散についての詳しい解説は上のリンクから解説をご確認下さい。
不偏分散
分散は標本分散のほかに不偏分散というも存在しています。この分散については触れたことのない人が多いと思います。
不偏分散とは、標本の偏りを除いて母集団の分散を推定することです。そして、不偏分散は母集団の分散を推定するために用いられる分散になっています。
抽出された標本は偏りを持っていて、この偏りを除いて母集団の分散を推定するために分母をN-1にしています。その為、不偏分散のことをN-1の分散と呼ぶ人も呼ぶ人もいます。
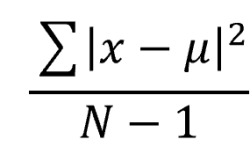
標本分散と不偏分散の違い
つまり、以下のような違いを持っているのです。
標本分散:標本のばらつきを表す
不偏分散:標本から偏りを除いて母集団の分散を推定するために表す
公式としては、不偏分散の分母がN-1で割ると覚えておきましょう。
まとめ
以上が「データサイエンス力」のNo.5の解説になります。
English
Explain that the population mean is different from the sample mean
It is significant to understand the difference between a sample and a population before explaining their means.
Population and sample
A population is a collection of persons, objects or items of interest whereas a sample is a portion of the whole and, if properly taken, is a representative of the whole.
Population mean
The population mean is represented by the Greek letter mu (μ). It is given by the formula:
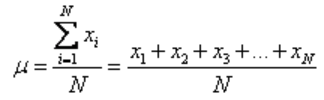
where N is the number of terms in the sample.
The capital Greek letter sigma () is commonly used in mathematics to represent a summation of all the numbers in a grouping. N is the number of terms in the population.
Sample Mean
The sample mean is represented by x bar . It is given by the formula:
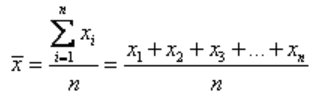
where n is the number of terms in the sample.
Purpose
Sample mean and population mean is used for data inference. In some (or maybe most) settings, the population is large but finite. However, often the population is so large (e.g., population of India) that we actually assume the population is infinite, to make some of the maths easier. Now the population is large, we usually cannot hope to calculate the parameter of interest (e.g., the population income mean/ average) exactly, because to do so we would have to obtain income information from the large population. This is often infeasible due to costs or practicalities.
Instead, we take a sample from the population of interest, and calculate the mean of the sample (or, more generally, an estimate of mean income of the sample, based on the sample data), giving the sample income mean. Now of course the sample mean will not equal the population mean. However, if the sample is a simple random sample, the sample mean is an unbiased estimate of the population mean. This means that the sample mean is not systematically smaller or larger than the population mean [7b]. Or put another way, if we were to repeatedly take lots and lots (actually an infinite number) of samples, the mean of the sample means would equal the population mean.




