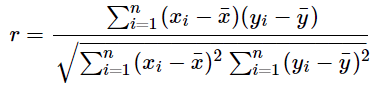相関係数について解説します。
この範囲は「データサイエンティストのためのスキルチェックリスト」の「データサイエンス力」項目No.9の解説になります。
多くの専門用語や公式が登場しますが丁寧に理解しやすく説明していきます。
本記事はデータサイエンスを研究されているIffat Maabさんによる英語の解説を翻訳しています。
Iffat Maab
東京大学大学院工学系研究科技術経営戦略学専攻(TMI)博士課程在学中。パキスタン、イスラマバード市出身
マーケターのためのデータサイエンスの時間とは?
こちらの講座では、一般社団法人データサイエンティスト協会様がリリースしている「データサイエンティストのためのスキルチェックリスト」に沿った解説を行っていきます。
「データサイエンティストのためのスキルチェックリスト」とは、データサイエンティストとして活躍するために必要なスキルが体系化されたものです。
このマーケターのためのデータサイエンスの時間に従って学習していくと、データサイエンティストに必要なスキルセットである「データサイエンス力」を一通り学習することが出来ます。
<マーケターのためのデータサイエンスの時間の全一覧はこちら>
一般的な相関係数(ピアソン)の分母と分子を説明できる
解説
今回は相関係数の分母と分子についてです。このことは相関係数の求め方を知ることで理解できます。
「一般的な相関係数(ピアソン)」と書かれていますが、前提として一般的な相関係数はピアソンの相関係数と呼ばれるものであるという点を覚えておきましょう。
相関係数とは
はじめに相関関係とはある事象が他の事象をどのように変化させるかという関係を示したものです。
この相関関係については第9回で解説しているのでご確認下さい、
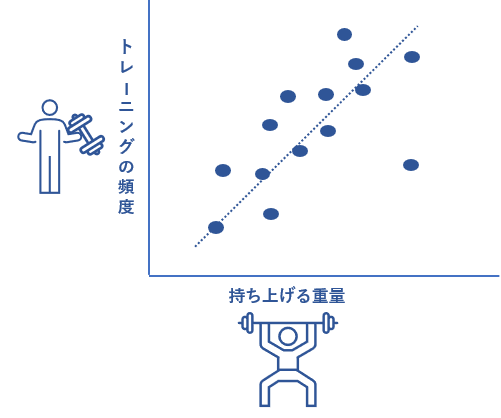
この相関関係の強さを数値化したものが相関係数になります。
相関係数の求め方
そして、相関係数はこの公式で求めることが出来ます。
![]()
r は相関係数で、決定係数 r²と直接関係しています。
rの符号は、推定傾斜係数b1の符号に依存する。
b1が負であれば、rは負の符号をとります。
b1が正であれば、rは正の符号をとります。
このことから、推定傾きと相関係数rは常に同じ符号を持つことがわかります。
また、r2は0から1の間の値をとるのに対し、相関係数rは常に-1から1の間の数値をとります。rの利点の一つは、単位がないことで、研究者は単位やスケールの異なるデータセットに相関係数を簡単に使用することができます。
このことは、rの代替式で簡単に理解できます。
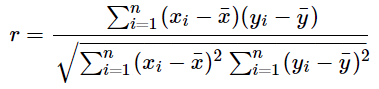
相関係数から相関の強さを判断
求められた相関係数によって相関の強さを以下の表から確認することが出来ます。
1.0に近づくほど正の相関があり、-1.0に近づくほど負の相関を持っています。
| 相関係数 | 相関の強さ |
| 0.7≤r≤1.0 | 強い正の相関 |
| 0.4≤r<0.7 | 正の相関 |
| 0.2≤r<0.4 | 弱い正の相関 |
| -0.2≤r<0.2 | ほどんど相関がない |
| -0.4≤r<-0.2 | 弱い負の相関 |
| -0.7≤r<-0.4 | 負の相関 |
| -1.0≤r<-0.7 | 強い負の相関 |
参考文献
[11] https://online.stat.psu.edu/stat462/node/96/
まとめ
以上が「データサイエンス力」のNo.9の解説になります。
English
Explain the denominator and numerator of a general correlation coefficient (Pearson)
Correlation tells a relation about how one thing changes another. It is an abstract math concept. It is denoted as:
![]()
‘r’ is the correlation coefficient which is directly related to the coefficient of determination ‘r2’.
The sign of r depends on the sign of the estimated slope coefficient b1
- If b1 is negative, then r takes a negative sign.
- If b1 is positive, then r takes a positive sign.
This shows that the estimated slope and the correlation coefficient r always share the same sign. Also, r2 has a value between 0 and 1, whereas the correlation coefficient r is always a number between -1 and 1.
One advantage of r is that it is unitless, allowing researchers to easily use correlation coefficients on different data sets with different units or scales. This can easily be understood by an alternative formula for r, as: