条件付き確率について解説します。
この範囲は「データサイエンティストのためのスキルチェックリスト」の「データサイエンス力」項目No.2の解説になります。
多くの専門用語や公式が登場しますが丁寧に理解しやすく説明していきます。
本記事はデータサイエンスを研究されているIffat Maabさんによる英語の解説を翻訳しています。
Iffat Maab
東京大学大学院工学系研究科技術経営戦略学専攻(TMI)博士課程在学中。パキスタン、イスラマバード市出身
マーケターのためのデータサイエンスの時間とは?
こちらの講座では、一般社団法人データサイエンティスト協会様がリリースしている「データサイエンティストのためのスキルチェックリスト」に沿った解説を行っていきます。
「データサイエンティストのためのスキルチェックリスト」とは、データサイエンティストとして活躍するために必要なスキルが体系化されたものです。
このマーケターのためのデータサイエンスの時間に従って学習していくと、データサイエンティストに必要なスキルセットである「データサイエンス力」を一通り学習することが出来ます。
条件付き確率の意味を説明できる
解答
条件付き確率とは【ある事象が起こるという条件のもとで別のある事象が起こる確率】のことです。
事象Aが発生している場合に、事象Bが発生する確率は以下の公式で求められます。
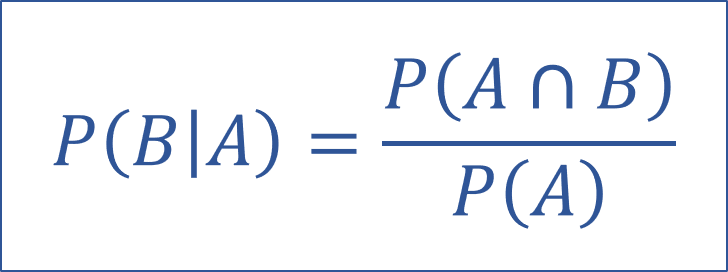
解説
まず条件付き確率を説明する前に、確率論の基礎となる”事象”と”標本空間”について解説します。
事象
事象とは、確率論において試行の結果に起こる事を言います。
他の事象の例としては、「コインを2回投げた」時の結果として、
表・表、表・裏、裏・裏 という事象が存在しています。
標本空間
標本空間とは、起こり得る全ての事象から成る集合のことを指します。
例えば「今日は何曜日ですか」という質問では月曜日から日曜日までの計7つの起こりうる事象があります。
この7つの事象の集合が標本空間です。

条件付き確率
ある事象が起こるという条件のもとで、別のある事象が起こる確率のことです。
例えば、「ある人が風邪をひいている」という事象Aは、「他の人を感染させる」という事象Bを引き起こす確率を持っています。
この場合に「ある人が風邪をひいている」上で「他の人を感染させる」確率は条件付き確率になります。
条件付き確率の公式
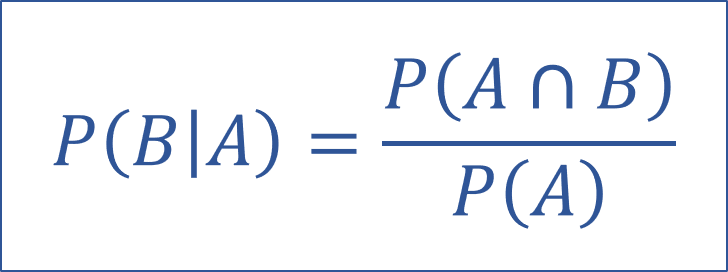
事象Aが発生している状況で事象Bが発生する条件付き確率は、P(B❘A)で表されます。
Pは”Probability”、日本語で「可能性」の頭文字です。
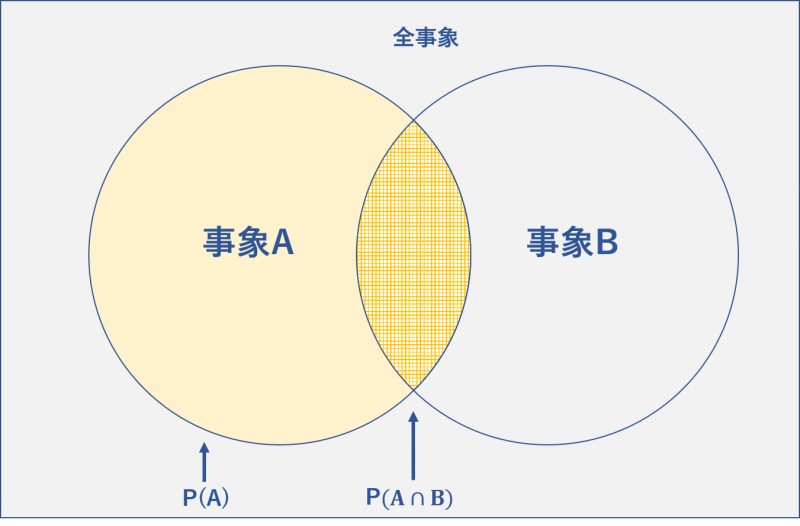
ここで、事象Aが起こる確率であるP(A)が条件付確率の分母であることが上の式から分かります。
そして、分子のP(A∩B)は事象AとBの両方が発生する確率です。
AとBの両方が発生する確率からBが発生する確率を割ることで条件付き確率を求めることが出来ます。
条件付き確率の問題例
最後に、具体的な問題から条件付き確率についてより深く理解しましょう。
問題
「袋の中に赤と青のビー玉が入っています。そこで、2個のビー玉を入れ替えなしで引きます。
赤いビー玉と青いビー玉が同時に選ばれる確率は0.28です。
最初の抽選で赤いビー玉が選ばれる確率は0.5です。
最初に引いたビー玉が赤であった場合、2回目の抽選で青のビー玉が選ばれる確率はいくらになるでしょうか」
問題参考:OnlineMathLearning.com|Conditional Probability
解答
この例題では、赤と青の両方のビー玉が選ばれる確率P(青∩赤)は0.28です。
しかし、最初に引いたビー玉が赤だったので、P(赤)は0.5の確率で独立事象となります。
ここで、2回目の抽選は、赤いビー玉の1つがすでに取り出されているので、1回目の抽選に依存しています。
P(青| 赤 ) は条件付き確率となり、以下のように計算されます。
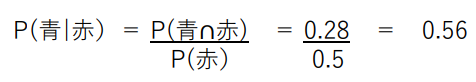
答え 0.56
まとめ
以上が「データサイエンス力」のNo.2の解説になります。
English
Explain the meaning of conditional probabilities
Event: In probability theory, an event is an outcome of a random experiment.
Sample space: All the possible outcomes of an event forms the sample space of an event/ experiment.
For example, what day of a week is today? has seven possible outcomes i.e., all days of a week which is called a sample space of an event. However, the possible outcome for a certain day is only one, so this outcome is called an event.
Conditional Probability
Events can be dependent or independent of one another. Conditional probability is the probability of an event given that the other event has already occurred.
For example, an event that a person is Covid-19 positive (first event already occurred) will have a chance that the event of making other people infected (dependent second event) is possible. So the chance of the people getting infected (second event) from a positive Covid-19 patient (first event) is a dependent event.
Formula for Conditional Probability
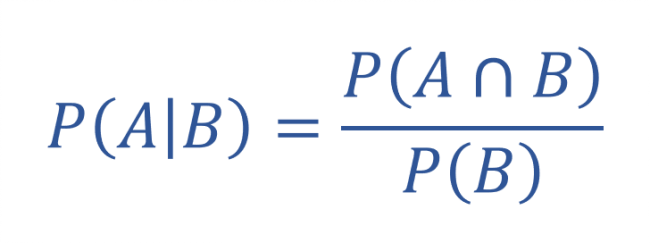
- P(A|B) is called the conditional probability; the probability of occurrence of event A (making other people infected i.e., dependent event) given that event B (the person has positive Covid-19 i.e., independent event) has already occurred. You can notice here that the independent event B i.e., P(B) is the denominator of conditional probability.
- P(A ∩ B) is the the joint probability of the occurrence of both events A and B; the probability that both events A and B occur. In some books, P(A ∩ B) is written as P(A and B) because the intersection is an AND operator in set theory.
- P(B) is the the probability of event B
Example of marbles
A bag contains red and blue marbles. Two marbles are drawn without replacement. The probability of selecting a red marble and a blue marble is 0.28. The probability of selecting a red marble on the first draw is 0.5. What is the probability [4a] of selecting a blue marble on the second draw, given that the first marble drawn was red?
Solution
In the given example, you can see that the probability of occurrence of the both the red and blue marble, P(Blue ∩ Red) is 0.28. However, it is mentioned that the first draw of selecting a marble is red so P(Red) becomes the independent event with the probability value of 0.5. Now, the selection of second draw depends on the first draw because one of the red marble is already taken out so the second draw (event) is dependent on the first P(Blue| Red ) becomes the conditional probability which is calculated below:
| P(Blue| Red) | = |
P(Blue ∩ Red) P(Red) |
= |
0.28 0.5 |
= | 0.56 |
Purpose
One of a real example of conditional probability can help illustrate the purpose of its usage. Suppose a voter poll is taken in three states. In state A, 50% of voters support the liberal candidate, in state B, 60% of the voters support the liberal candidate, and in state C, 35% of the voters support the liberal candidate. Of the total population of the three states, 40% live in state A, 25% live in state B, and 35% live in state C. Given that a voter supports the liberal candidate, what is the probability that he/ she lives in state B? [4b]
By conditional probability,
P(Voter lives in state B| Voter supports liberal candidate) =
P(Voter supports liberal candidate| Voter lives in state B)P(Voter lives in state B)/
(P(Voter supports lib. cand.| Voter lives in state A)P(Voter lives in state A) +
P(Voter supports lib. cand.| Voter lives in state B)P(Voter lives in state B) +
P(Voter supports lib. cand.| Voter lives in state C)P(Voter lives in state C))
= (0.60)*(0.25)/((0.50)*(0.40) + (0.60)*(0.25) + (0.35)*(0.35))
= (0.15)/(0.20 + 0.15 + 0.1225) = 0.15/0.4725 = 0.3175
The probability that the voter lives in state B is approximately 0.32.
References
[4a]https://www.onlinemathlearning.com/conditional-probability.html
[4b]http://www.stat.yale.edu/Courses/1997-98/101/condprob.html



