情報量とエントロピーについて解説します。
この範囲は「データサイエンティストのためのスキルチェックリスト」の「データサイエンス力」項目No.15の解説になります。
多くの専門用語や公式が登場しますが丁寧に理解しやすく説明していきます。
本記事はデータサイエンスを研究されているIffat Maabさんによる英語の解説を翻訳しています。
Iffat Maab
東京大学大学院工学系研究科技術経営戦略学専攻（TMI）博士課程在学中。パキスタン、イスラマバード市出身
マーケターのためのデータサイエンスの時間とは？
こちらの講座では、一般社団法人データサイエンティスト協会様がリリースしている「データサイエンティストのためのスキルチェックリスト」に沿った解説を行っていきます。
「データサイエンティストのためのスキルチェックリスト」とは、データサイエンティストとして活躍するために必要なスキルが体系化されたものです。
このマーケターのためのデータサイエンスの時間に従って学習していくと、データサイエンティストに必要なスキルセットである「データサイエンス力」を一通り学習することが出来ます。
自己情報量やエントロピーの意味について説明できる
解答
自己情報量とは情報量の大きさを定量化した数値のことである。そして、エントロピーは情報の不確実性の大きさを表す量のことである。
解説
機械学習の分野においては、情報量を定量化して定義します。
そもそも、日常生活において情報とは「明日の天気は晴れ」や「近所に新しいレストランが出来た」というようなものでありその情報量の大きさを数値で測ることはありません。
しかし、数値で表せられなければ機械学習で情報を扱うことが困難になってしまいます。
そこで、情報量の大きさをあいまいな概念から数値へと定量化させて表すことによって数学的に扱うことを可能にするのです。
自己情報量
自己情報量は「情報量」を数値で表すために用いられています。
そこで、定量化された情報量として表すために以下の公式が用いられています。
| I (x) = – log P(x) |
事象xが起こる確率がP(x)であり、それの対数をマイナスで表したものになっています。
また、この公式を見てみると、
| I (x) = – log P(x) |
P(x)が含まれていることから確率の関数になっていることが明らかになっています。また、この公式をグラフ化すると以下のような減少関数になります。
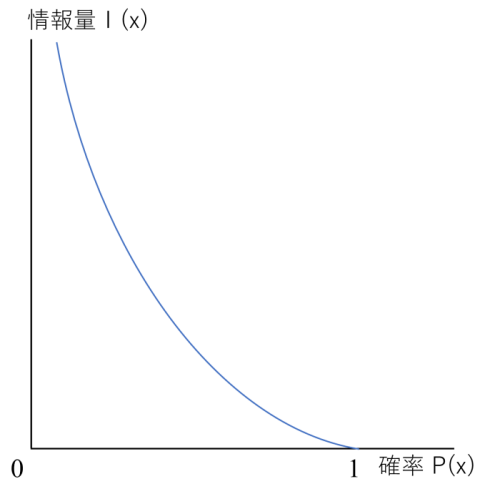
それでは、情報量はなぜ確率が増えると減少するのでしょうか。
例えば、1~30までの数字があるルーレットで「A: 1~20が出た」と「B: 7が出た」の情報があるとします。
Aの確率は2/3でBの確率は1/30であるため、Bの方が確率が低いことは明らかです。
そのため、Bの確率はＡと比べて「珍しい」という点で情報量は多くなっています。
従って、グラフから分かるように確率が低いほど情報量は多くなっているのです。
以上のように、自己情報量については (x) = – log P(x)の公式を覚え、確率が１に近づくほど情報量が減少する減少関数であるという特徴を覚えることが大切になっています。
エントロピー
次に、(情報)エントロピーについてです。
エントロピーは平均情報量とも呼ばれており、情報の乱雑さや不確実さを表している量のことです。同時に、このことは情報源から出る情報量の平均を自己情報量の期待値としても扱われています。
つまり、エントロピーとは情報が不確実で乱雑であればあるほど、平均としてその情報は多くの情報を運んでいるということになります。
そのため、「情報が乱雑でその情報から将来何が起こるかが不確実」であればあるほど「情報エントロピーが高い」と呼びます。
- 情報が乱雑で将来が予測できない → エントロピーが高い
- 情報が整っている → エントロピーが低い
ということになります。
つまり、エントロピーに関しては情報の不確実性が大きいとエントロピーは高くなるということを覚えておくことが大切になっています。
まとめ
以上が「データサイエンス力」のNo.15の解説になります。