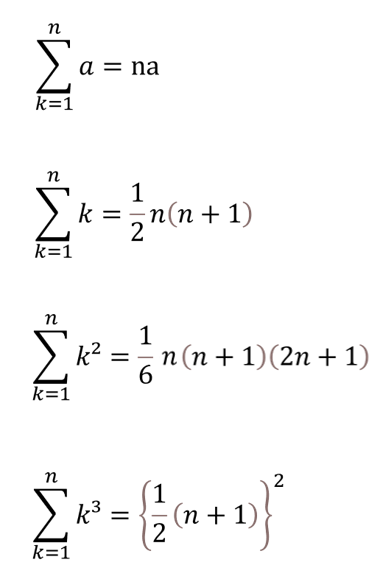∑（シグマ）の計算方法【マーケターのためのデータサイエンスの時間】

Σ（シグマ）の計算方法について解説します。

多くの専門用語や公式が登場しますが丁寧に理解しやすく説明していきます。

本記事はデータサイエンスを研究されているIffat Maabさんによる英語の解説を翻訳しています。

 

Iffat Maab

東京大学大学院工学系研究科技術経営戦略学専攻（TMI）博士課程在学中。パキスタン、イスラマバード市出身

---

マーケターのためのデータサイエンスの時間とは？

こちらの講座では、一般社団法人データサイエンティスト協会様がリリースしている「データサイエンティストのためのスキルチェックリスト」に沿った解説を行っていきます。

「データサイエンティストのためのスキルチェックリスト」とは、データサイエンティストとして活躍するために必要なスキルが体系化されたものです。

 

このマーケターのためのデータサイエンスの時間に従って学習していくと、データサイエンティストに必要なスキルセットである「データサイエンス力」を一通り学習することが出来ます。

＜マーケターのためのデータサイエンスの時間の全一覧はこちら＞

---

1 + 4 + 9 + 16 + 25 + 36 は、Σを用いて表すことができる。

解答

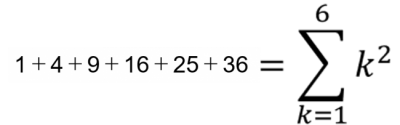
解説

この問題はΣ（シグマ）を用いた計算方法についてです。

Σとは総和を表すために用いられる文字式です。非常に長く複雑な数列を計算する際に用いることで、短く分かりやすく表すことが出来ます。

この問題で与えられた数列を見ると「1、4、9、16」のように、どの数字も自然数の平方であることが分かります。

そこで、Σを用いてこの数列を表すために、はじめにこの数列を一般化します。今回の数列では k² と一般化することが出来ます。

次に、項数(数列の項の数)を数え、足し始めから足し終わりを以下のようにΣの上下に書くことで、数列をΣで表すことが出来ます。

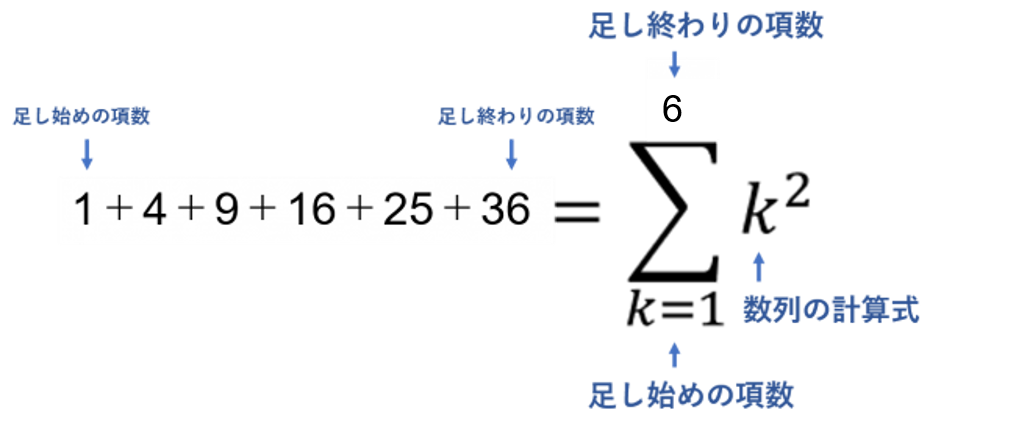
（まとめ）Σでの表し方

1. 与えられた数列の一般化
2. 項数の把握

 

補足｜Σの計算方法

基本的なΣの計算をする際には以下の公式を覚えておく必要があります。

先ほど、表した k² の式では上から３つ目の公式に当てはめて計算することが出来ます。

---

おわりに

以上が「データサイエンス力」の基礎となる∑（シグマ）です。

 

---

English

A simple representation of the sum of series formula is represented as 

 x0, x1, x2, …,  xn 

where x0, x1, x2, … represents the elements in a sample. The summation is calculated by taking the sum Σ of all values of a given sample as shown in the formula above i.e., 

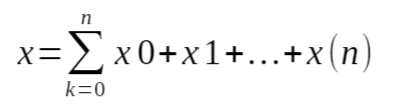
or for the given sequence in the question we can simply transform the formula using 

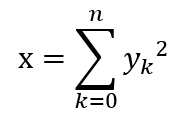
where (n) is the total number of elements in the set (y), (k) is an iterative variable that sums every next number with its previous number, and (y) is the actual set of numbers. The result (x) is the output in the form of sum of squares.

This is because If you look closely at the numbers in the given case, you will find out that every number is a perfect square of the first six natural numbers. Hence, a more generalized representation of the given numbers can be shown in the series formula above.  

By using the above formula, we have 

• Total number of elements, n = 6
• The elements in a set y = {1, 2, 3, 4, 5, 6} correspondingly means

y0 = 1, y1 = 2, y2 = 3, y3 = 4, y4 = 5,  y5 = 6, i.e., the first six natural numbers 

• The total sum (x) = ?

Now the summation (x) can be calculated as shown:

            x = Σ (y02 + y12  + y22  + y32 + y 42 + y52)

    x = Σ (12 + 22  + 32  + 42 + 52 + 62)

x = Σ (1 + 4 + 9 + 16 + 25 + 36)

                                             x = 91

There are many infinite sequence formulas, like sum of cube squares, sum of under roots, sum of any number power etc.